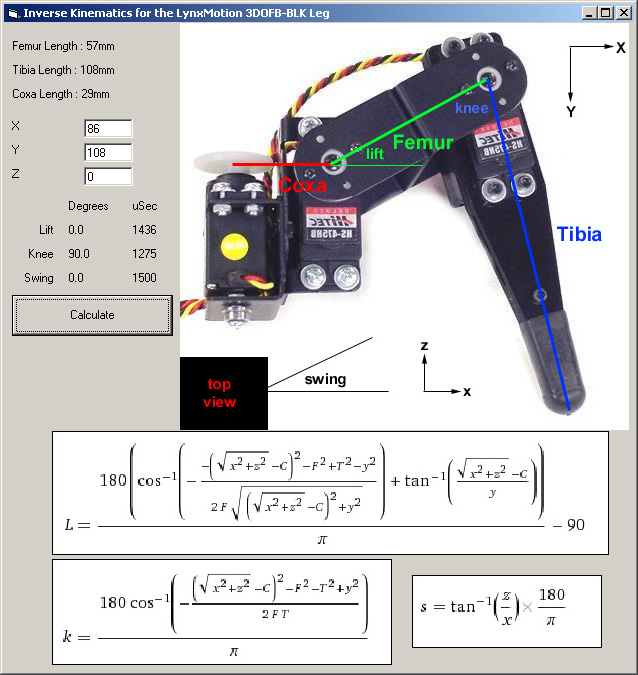
I wanted to write my own code to control my new hexapod and I found it a little difficult to find a simplified set of IK equations, so thought I would post them here in case others are having similar issues.
I used this website as a guide in case anyone wanted a better explanation of the derivation of the equations. I am using VB6 right now, just because I am more comfortable with it, but the simplified equations are the obviously important part.
arduin0.blogspot.com/2012/01/inverse-kinematics-ik-implementation.html
These equations should be valid for almost all 3dof legs, but I am using the lynxmotion 3DOFB-BLK leg if anyone is interested.
lynxmotion.com/p-550-3dof-al … ervos.aspx
[code]Private Sub Command1_Click()
'inputs
pi = 3.14159265359
femurlength = 57
tibialength = 108
coxalength = 29
x = Val(Text3.Text)
y = Val(Text4.Text)
z = Val(Text5.Text)
'calculations
knee = ACos(((Sqr(((Sqr(x ^ 2 + z ^ 2)) - coxalength) ^ 2 + y ^ 2)) ^ 2 - tibialength ^ 2 - femurlength ^ 2) / (-2 * femurlength * tibialength)) * 180 / pi
swing = Atn(z / x) * 180 / pi
lift = (((Atn(((Sqr(x ^ 2 + z ^ 2)) - coxalength) / y)) + (ACos((tibialength ^ 2 - femurlength ^ 2 - (Sqr(((Sqr(x ^ 2 + z ^ 2)) - coxalength) ^ 2 + y ^ 2)) ^ 2) / (-2 * femurlength * (Sqr(((Sqr(x ^ 2 + z ^ 2)) - coxalength) ^ 2 + y ^ 2)))))) * 180 / pi) - 90
'display
Label10.Caption = FormatNumber(lift, 1)
Label11.Caption = FormatNumber(knee, 1)
Label12.Caption = FormatNumber(swing, 1)
Label13.Caption = 1436 + 9.7 * CInt(lift)
Label14.Caption = 402 + 9.7 * CInt(knee)
Label15.Caption = 1500 + 9.7 * CInt(swing)
End Sub
’ arc sine
’ error if value is outside the range -1,1]
Function ASin(value As Double) As Double
If Abs(CDbl(Val(value))) <> 1 Then
ASin = Atn(value / Sqr(1 - value * value))
Else
ASin = 1.5707963267949 * Sgn(value)
End If
End Function
’ arc cosine
’ error if NUMBER is outside the range -1,1]
Function ACos(ByVal number As Double) As Double
If Abs(CDbl(Val(number))) <> 1 Then
ACos = 1.5707963267949 - Atn(number / Sqr(1 - number * number))
ElseIf number = -1 Then
ACos = 3.14159265358979
End If
'elseif number=1 --> Acos=0 (implicit)
End Function[/code]
Variables in the attached screenshot equations are as follows:
L - Lift servo angle from horizontal
k - knee servo angle
s - horizontal servo swing angle
x - x foot position in mm
y - y foot position in mm
z - z foot position in mm
C - Coxa length
T - Tibia length
F - Femur Length
vb uses radians for all its calculations, so rad*180/pi will convert back to degrees, which is already in these equations.
Again, this is nothing new, but I figured if it took me as long as it did to get these simplified and working others might be struggling with the same issue either now or in the future.