February 12, 2015
A single artificial neuron can represent some simple Boolean functions like OR, AND or NAND and some like XOR not, because a single artificial neuron can only learn linearly separable mappings.
Example. Perceptron for the AND function:

Now, the question I am interested in is: can we build a hardware artificial neuron with a set of logic gates?
Let's say we have a set of the 6 basic logic gates AND, OR, NAND, NOR, XOR and XNOR. We apply the first sample of a 2-dimensional binary training input vector (but we could extend every of those logic gates to n-dimensional inputs) to the logic gates inputs at the same time and compare the first binary output sample from the training set with the actual output of every gate. If the output of the training set is equal to the output of a gate, we keep it in the set, otherwise we remove it from the set (simply disable the gate or set its output continuously to LOW). At the end of the training should be the correct gate left.
A big advantage over the common single artificial neuron design would be that it could learn nonlinearly separable mappings as well.
I am not totally done with the design of the gate disabling part (I plan to use D or RS FlipFlops and AND gates to multiply the Boolean error with the output), but I managed to design the necessary gate output comparator. If the gate output is equal to the actual training set output, the output of the according XNOR gate (XOR gate with inverting output) goes HIGH (output true), else LOW (output false). I am using a software called LogicSim to simulate the logic gate circuit.
February 13, 2015
I managed to design the gate disabling part as well. The video shows the artificial neuron learning to act as a NAND and XOR gate. After learning is finished, the
![]()
Schematic of a single FLGA below:
The FLGA only memorizes the output state of a logic gate if it is false. Then the outpute state will be set continuously to LOW. This works as follows:

As long as the 'Save data' labeled pin (and 'Reset' labeled pin) is LOW the output pin (connected to the LED) state is equal to the 'Data' labeled input pin. If the 'Data' input pin is HIGH and the 'Save data' pin is HIGH, the D FlipFlop does not store the logical 1 'Data' bit because of the NOT gate connected to the AND gate input on the left side. Only if the 'Data' pin is LOW and the 'Save' data pin is HIGH, the according logical 1 'Data' bit is stored by the D FlipFlop. At the same time the D FlipFlop is locked up because of the LOW-HIGH transition of the 'CK' labeled input pin of the D FlipFlop, which is connected to its 'D' labeled input pin. The FlipFlop can only be unlocked by a LOW-HIGH transition of the 'Reset' pin. Now actually the stored logical 1 'Data' bit should be a logical 0 'Data' bit, so we use the inverted output of the D FlipFlop. One input of the second AND gate on the right side is connected to inverted output of the D FlipFlop and the other input to the 'Data' pin. Whatever the state of the 'Data' input pin after storage is, the output of the AND gate on the right side will be always LOW because the AND gate input connected to the inverted output of the D FlipFlop is LOW.
February 14, 2015
A remaining question is how many training samples we actually need to determine the correct gate. The truth table for all of the logic gates looks as following:
x1 | x2 | AND y | OR y | NAND y | NOR y | XOR y | XNOR y |
0 | 0 | 0 | 0 | 1 | 1 | 0 | 1 |
0 | 1 | 0 | 1 | 1 | 0 | 1 | 0 |
1 | 0 | 0 | 1 | 1 | 0 | 1 | 0 |
1 | 1 | 1 | 1 | 0 | 0 | 0 | 1 |
We can see in every output row we have the same number of ones and zeros – 3. That means we can exclude 3 gates by the first training input sample (0,0).
x1 | x2 | AND y | OR y | XOR y | NAND y | NOR y | XNOR y |
0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 |
0 | 1 | 0 | 1 | 1 | 1 | 0 | 0 |
1 | 0 | 0 | 1 | 1 | 1 | 0 | 0 |
1 | 1 | 1 | 1 | 0 | 0 | 0 | 1 |
On the second table we can see already that it would only take the second input sample (0,1) to train the neuron if the desired gate is an AND or NAND. However neither we nor the neuron knows at that stage what the correct gate is, so there are maximal two possible gates left after the second training input sample. The third input sample (1,0) can be neglected, because the outputs of the remaining gates at this training input sample are equal to outputs of the prior training input sample. Instead we are applying directly the fourth training input sample (1,1) to determine the correct gate.
February 15, 2015
Found a much simpler design with the same function described above. One difference though: All four training input samples must be applied. This is in the end a FPGA. It is not able to learn. All possible input combinations must be applied and memorized.
February 16, 2015
Finally I want to describe the artificial neuron above mathematically.
Equivalent network (example):
Therefore we define:
-
is the set of

binary logic gate outputs where
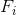
is the
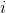
th logic gate output
-
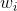
is the weight of the
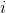
th logic gate output
-
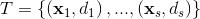
is the training set of

samples where
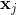
is the
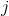
th n-dimensional input vector,
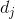
the desired output,
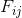
the
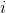
th logic gate output for that input vector and
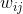
the according weight for that logic gate output
-
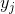
denotes the binary output of the neuron for an input vector
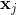
The actual output of the neuron is given by

The circled dot product is the Boolean expression of the error and can be written as
![]()
Hence

An activation function is not necessary because
![]()
Weights are initialized to 1 and then updated according to following rule
![]()
February 17, 2015
There are still some pieces missing as the suggested neuron can't emulate all possible output permutations. About how many we are talking? Well, we have two possible numbers (n), 0 and 1 and we have 4 outputs (r) for the 4 training input vectors. The order of the numbers is important and we can repeat a number, so we have obviously following possible permutations:
![]()
And these are the missing candidates:
x1 | x2 | Y7 | Y8 | Y9 | Y10 | Y11 | Y12 | Y13 | Y14 | Y15 | Y16 |
0 | 0 | 0 | 0 | 1 | 1 | 0 | 1 | 0 | 0 | 1 | 1 |
0 | 1 | 0 | 1 | 1 | 0 | 0 | 1 | 0 | 1 | 0 | 1 |
1 | 0 | 1 | 0 | 0 | 1 | 0 | 1 | 1 | 0 | 1 | 0 |
1 | 1 | 1 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 1 |
The schematic for the neuron looks now as following. I have removed the XOR and XNOR stage. The reason is as follows: We have 16 possible permutations. 0’s and 1’s are equally distributed, so with every traning sample we exclude half of the remaining permutations. After the first training sample, 8 permutations are excluded, after the second training sample 4, after the third training sample 2, after the fourth training sample 1. There would be no chance that the neuron recognizes the AND or OR function only after 3 training samples. No learning would take place. Having only 14 elements in the set of binary logic gate outputs (the same as a perceptron can emulate) changes things dramatically because 0’s and 1’s aren’t equally distributed anymore. The neuron is now able to emulate the AND, OR and NOR function after only 3 training samples (video).
I am using a new software called Logisim to simulate the circuit. The nice thing on Logisim is that you can put a circuit in a virtual chip and copy this chip as often as you want. So it’s easy to simulate neural networks. Image I would need to copy this bulky schematic below 100’s of times!
February 20, 2015
By studying the state table below I noticed that I could simplify the neuron design dramatically by using a bias. The bias is set automatically by the first training sample. If the bias is 1, all inputs are inverted. This is done by XOR gates which can be used as controlled inverters.
x1 | x2 | y1 | y2 | y3 | y4 | y5 | y6 | y7 | y8 | y9 | y10 | y11 | y12 | y13 | y14 | Iteration |
0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
0 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 2 |
1 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 3 |
1 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 1 | 0 | 0 | 1 | 0 | 1 | 0 | 1 | 4 |
New schematic:
Video (shows classification of AND, OR and NOR in 3 iteration steps)








