Hi all, first, I have two versions of my question: 1) what is wrong with the way I am trying to calculate the Jacobian and then its pseudo inverse? 2) Does anyone have a good reference for how to solve for the next angles of each joint based on the velocity of the end effector and Jacobian?
Now some background: I am working on a hexapod and trying to design the inverse kinematics and path following for the individual legs. Because this will involve a lot of repletion/trial and error, I am designing a simulator to help me test my pathing so I don’t accidentally break something. I’ve laid the groundwork for a lot of it; drawing the robot, homogenous transform calculation, even calculating the Jacobian.
What I’m running into is trouble solving for the inverse Jacobian. The first time it’s calculated seems fine and the arm moves a little bit toward its target. The second time it’s calculated, the values go to extremes causing the arm to basically invert itself. The third and subsequent times, it seems fine. (See gif for example.)
I’ve reviewed formulas, not seeing any issue there. I’ve reviewed outputs and haven’t found anything out of the ordinary besides the pseudo inverse. And the visuals appear to make sense after the inversion of the arm.
I’ve done a lot of research for examples of inverse Jacobian math but can only find symbolic solutions.
Is there something I’m missing? Code provided below, I’ll mention this is in Ocatave/Matlab.
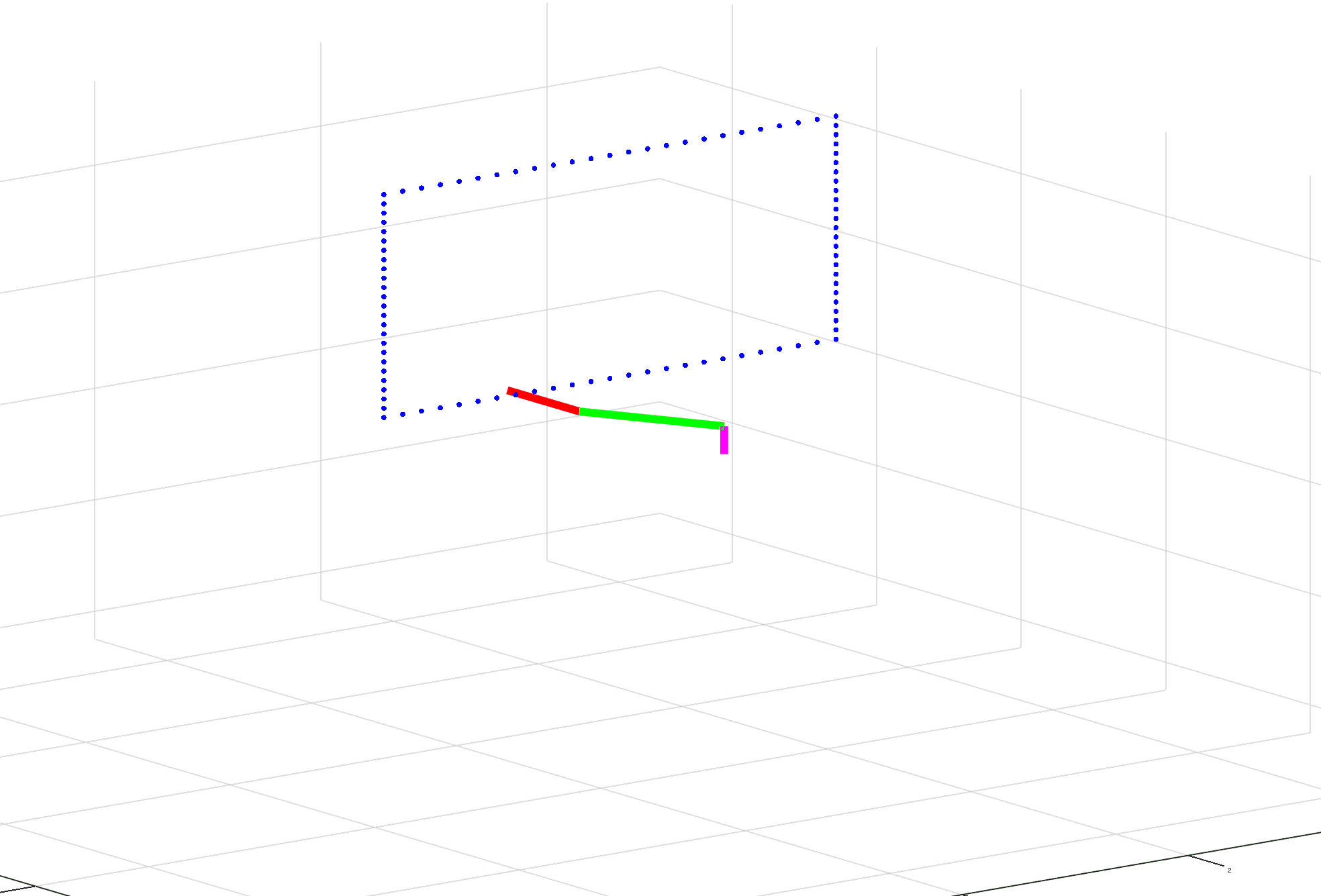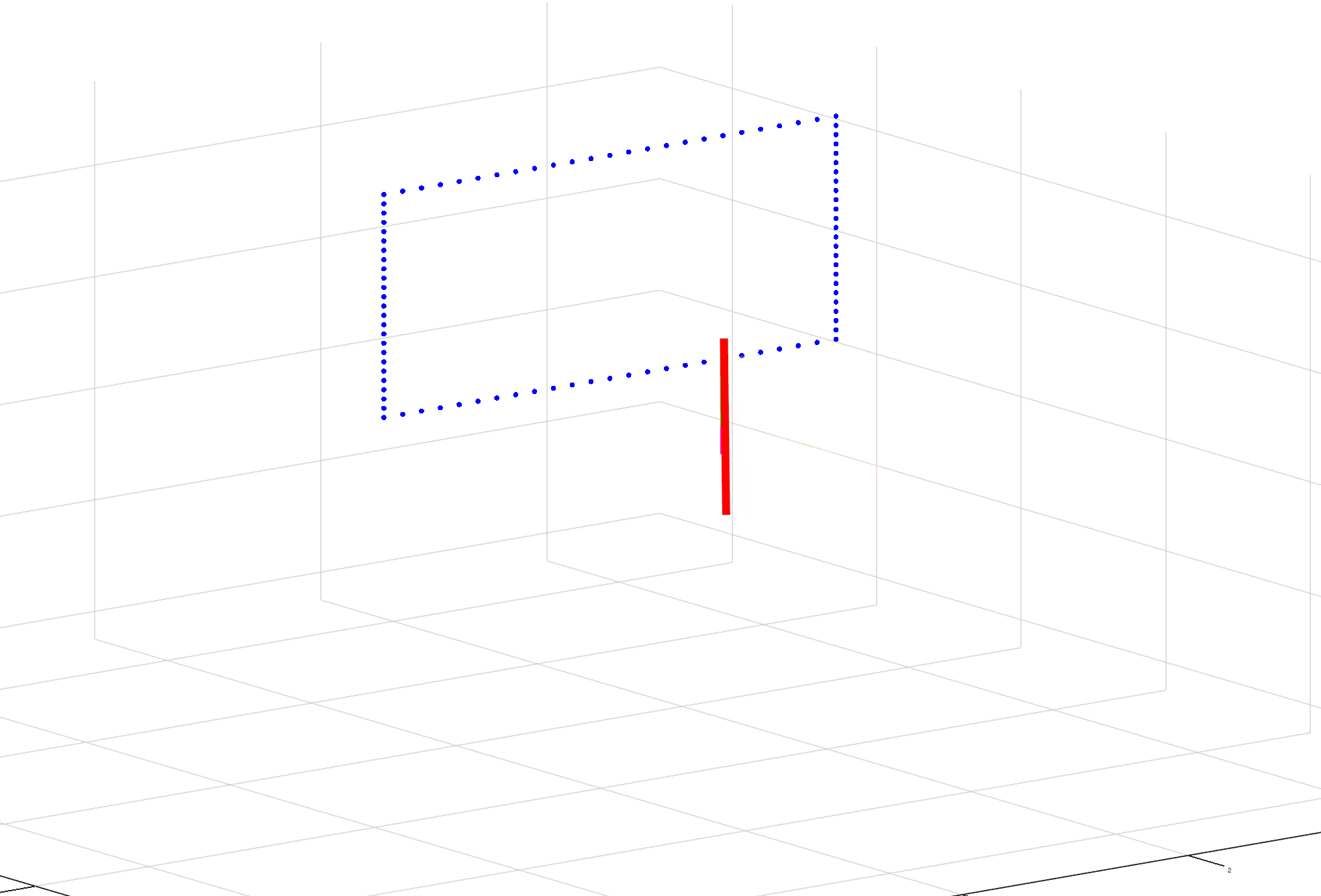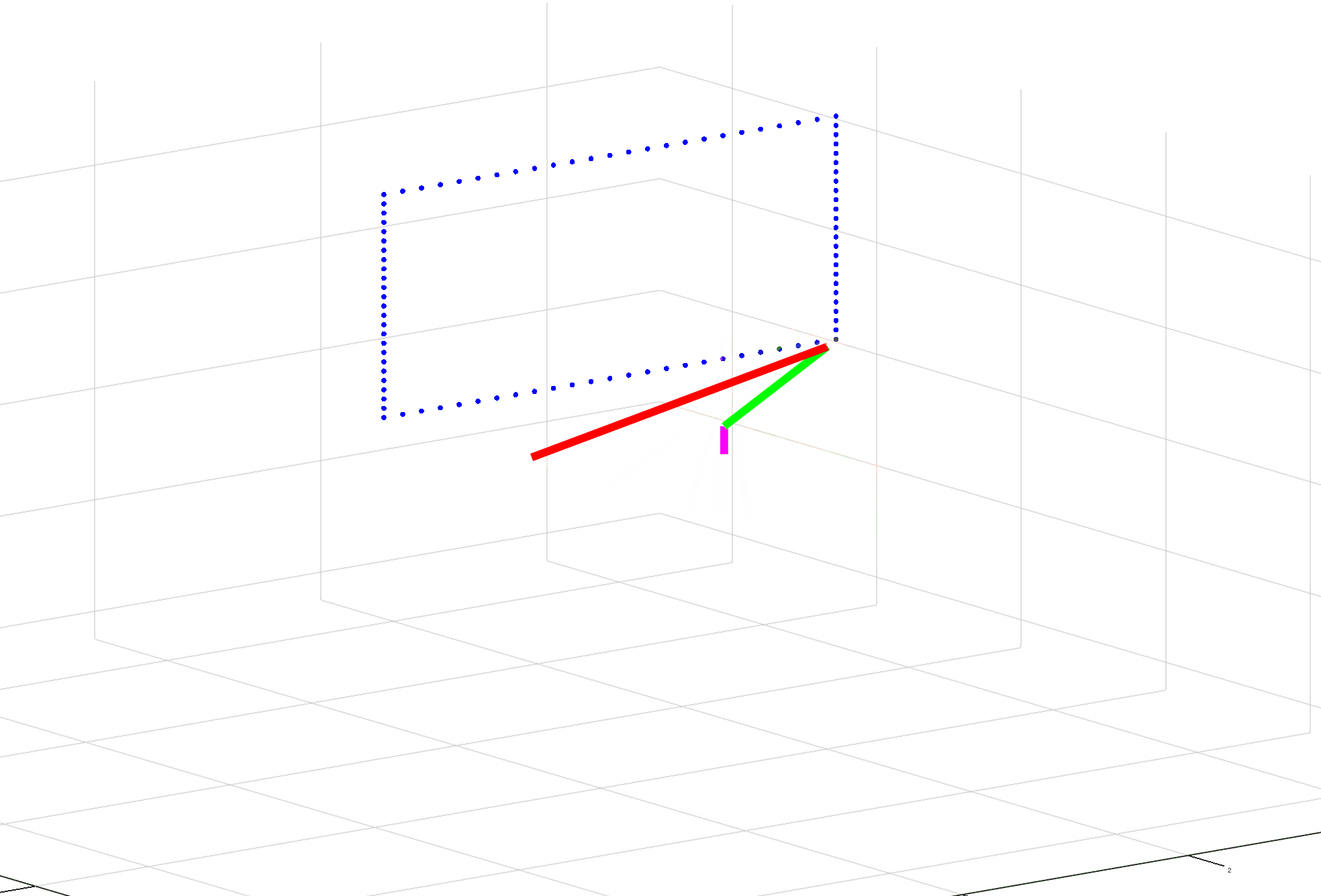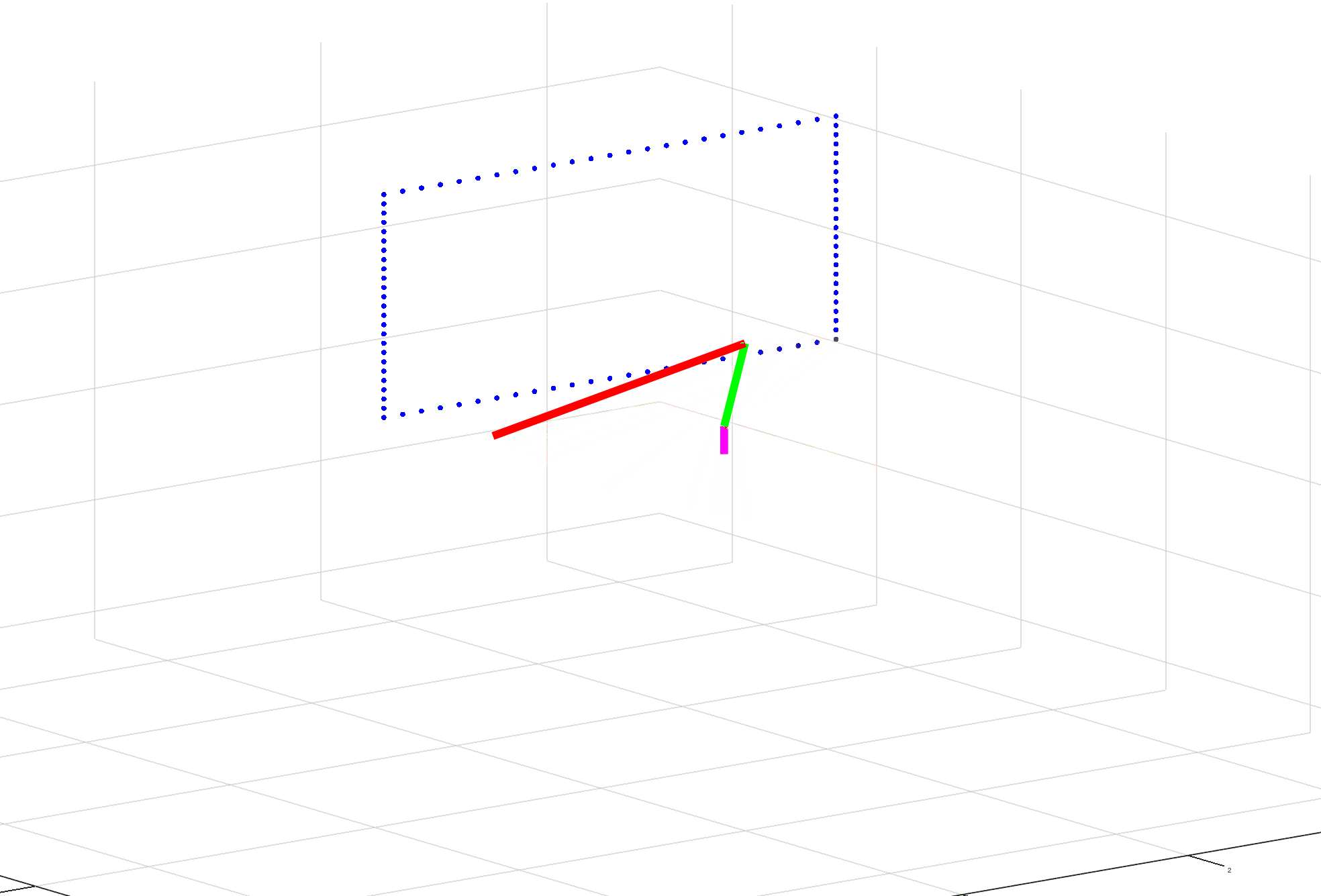
clc;
clear;
clearvars;
function H = Hg(th,a,r,d) % Creates homogenous transform
H = [cosd(th) -sind(th)*cosd(a) sind(th)*sind(a) r*cosd(th);
sind(th) cosd(th)*cosd(a) -cosd(th)*sind(a) r*sind(th);
0 sind(a) cosd(a) d;
0 0 0 1];
end
function drawLeg(t, xp, yp, zp, Body, CoxaS, FemurS, TibiaS, EndEfS)
CoxaV = [CoxaS(1), FemurS(1); CoxaS(2), FemurS(2); CoxaS(3), FemurS(3)];
FemurV = [FemurS(1), TibiaS(1); FemurS(2), TibiaS(2); FemurS(3), TibiaS(3)];
TibiaV = [TibiaS(1), EndEfS(1); TibiaS(2), EndEfS(2); TibiaS(3), EndEfS(3)];
plot3(xp, yp, zp, 'b.') %draw path
hold on
plot3(CoxaV(1,:), CoxaV(2,:), CoxaV(3,:), 'm', 'LineWidth', 3) %draw coxa
plot3(FemurV(1,:), FemurV(2,:), FemurV(3,:), 'g', 'LineWidth', 3) %draw femur
plot3(TibiaV(1,:), TibiaV(2,:), TibiaV(3,:), 'r', 'LineWidth', 3) %draw tibia
axis([Body(1)-5 Body(1)+5 Body(2)-5 Body(2)+7 Body(3)-5 Body(3)+5])
axis equal
%body centered graph to make sure it stays in view while walking
grid on
hold off
pause(t)
end
function [Th1, Th2, Th3] = stepLeg (t, Th1, Th2, Th3, x, y, z)
### DESIGN ROBOT ###
% 3DOF articulting arm
% Start with only z offset for center of robot.
x00 = 0;
y00 = 0;
z00 = .5;
% Link lengths
a0 = 2; %distance from body center to leg 1, UPDATE FROM CAD
a1 = .5; %length of coxa in cm aka base (joint 0) to joint 1 in z direction
a2 = 1; %length of femur
a3 = 1; %length of tibia
## DH Parameters ##
Th0 = 30; %UPDATE FROM CAD
A0 = 0;
A1 = 90;
A2 = 0;
A3 = 0;
r0 = a0;
r1 = 0;
r2 = a2;
r3 = a3;
d0 = 0;
d1 = a1;
d2 = 0;
d3 = 0;
## Build vectors for each segment ##
% Each line has an extra element to help the matrix math
Body = [x00; y00; z00; 1];
Coxa = [0; a1; 0; 1];
Femur = [a2; 0; 0; 1];
Tibia = [a3; 0; 0; 1];
## Generate all homogenous transforms ##
Hb0 = Hg(Th0, A0, r0, d0);
H01 = Hg(Th1, A1, r1, d1);
H12 = Hg(Th2, A2, r2, d2);
H23 = Hg(Th3, A3, r3, d3);
Hb1 = Hb0*H01;
Hb2 = Hb0*H01*H12;
Hb3 = Hb0*H01*H12*H23;
## Calculate starting locations for each segment ##
CoxaS = Hb0*Body;
FemurS = Hb0*H01*Coxa;
TibiaS = Hb0*H01*H12*Femur;
EndEfS = Hb0*H01*H12*H23*Tibia;
## Draw the leg ##
drawLeg(t, x, y, z, Body, CoxaS, FemurS, TibiaS, EndEfS)
### Now to give a target for the leg ###
## Generate Jacobian ##
# Rotation matrices #
Rbb = [1, 0, 0; 0, 1, 0; 0, 0, 1];
Rb0 = Hb0(1:3, 1:3); %use first three rows and first three columns
Rb1 = Hb1(1:3, 1:3);
Rb2 = Hb2(1:3, 1:3);
# Displacement vectors #
dbb = 0;
db0 = Hb0(1:3, 4); %use first three rows of fourth column
db1 = Hb1(1:3, 4);
db2 = Hb2(1:3, 4);
db3 = Hb3(1:3, 4);
# Joint rotation velocity matrices #
rbb = Rbb*[0;0;1];
rb0 = Rb0*[0;0;1];
rb1 = Rb1*[0;0;1];
rb2 = Rb2*[0;0;1];
# Create the culumns representing partial diffferentials for each joint #
%zeroth = [cross(rbb, db3-dbb); rbb] % not needed since it's a fixed joint
first = [cross(rb0, db3-db0); rb0];
second = [cross(rb1, db3-db1); rb1];
third = [cross(rb2, db3-db2); rb2];
# Concatinate into the jacobian #
fullJ = [first, second, third];
% only need the cartesian portion
J = fullJ(1:3, 1:3)
Jinv = pinv(J) %Print for troubleshooting
## Calculate the velocity of the end effector ##
EndEfS %Print for troubleshooting
TargetX = x(1) %Print for troubleshooting
TargetY = y(1) %Print for troubleshooting
TargetZ = z(1) %Print for troubleshooting
Err =[x(1); y(1); z(1); 0] - EndEfS %Print for troubleshooting
fullV = ([x(1); y(1); z(1); 0] - EndEfS)*t;% Calculate velocity of EE
V = fullV(1:3); % Removing the last element since it's trash info
# Calc new joint angles #
w = pinv(J)*V; % Calc joint velocities
delTh = w.'/t % Calc change in joint angles
Th0 = Th0; %this should never change?
Th1 = Th1 + delTh(1);
Th2 = Th2 + delTh(2);
Th3 = Th3 + delTh(3);
end
### TIME STEP ###
t = .001
### BUILD PATH ###
% test to determine how piecewise funcitons would work to create path.
% This square looks really nice for now
for i = 1:96
if i <= 24
x(i) = i/6;
y(i) = 3;
z(i) = 1;
elseif 24 < i && i <= 48
x(i) = x(i-1);
z(i) = z(i-1)+1/6;
y(i) = 3;
elseif 48 < i && i <= 72
x(i) = x(i-1) - 1/6;
z(i) = z(i-1);
y(i) = 3;
elseif 72 < i && i <= 96
x(i) = x(i-1);
z(i) = z(i-1) - 1/6;
y(i) = 3;
end
end
### Set Up Initial Angles ###
% Starting angles
Th1 = 60; %UPDATE FROM CAD
Th2 = 0;
Th3 = 0;
### Time Loop ###
for i = 1:10
[Th1, Th2, Th3] = stepLeg(t, Th1, Th2, Th3, x, y, z)
end

