Effectively Using the Sharp GP2D12 Rangefinder

In this article, Jean-Christophe shows you how to maximize the utility you get out of a Sharp GPD12 rangefinder.

• Overview:

  This application note is intended to provide a good overview of the Sharp
  GP2D12 sensor (Fig. 1) and its use, especially for dynamics application.
  I hope it will help robotists to avoid some pitfalls and make this sensor work more easily. This is one of the most commonly
  used range finders in autonomous robotics applications for hobbyists and also in academic
  research. The reasons for this are essentially its low price (about 14$
  at Acroname,
  for example), its compact (~40x14x13mm) and lightweight package (a
  comparison between several sensors may be found here). The GP2D12 is
  based on the triangulation
  principle with a collimated infrared LED for the emitting element and
  a PSD (Position Sensing Device) which constitutes
  the receiver.

Fig. 1 - Sharp GP2D12 distance sensor		Fig. 2- Sharp GP2D12 output pattern

Although there exists a very similar sensor with a digital output (the
GP2D02),
I will focus only on the GP2D12 which has an analog output (see Fig. 2). The
main motivation for this choice is that the digital version is almost twice
as slow than the GP2D12 (update period about 75ms against
40ms for the analog version). Table 1 gives a brief overview of the
GP2D12 specifications (Here is the full and
latest official datasheet).

Note: it is very important to put a good capacitor (something like 22uF)
between GND and Vcc, directly on the sensor itself, in order to reduce the
noise on the 5V power supply due to the current required by the emitting LED.
In the other hand, avoid the use of a capacitor between the signal output
and GND or Vcc: it may dramatically reduce the sensor dynamics (low pass filter).
Below, we will see how to numerically filter this output in order to improve
the precision without decreasing the dynamics.

• AD conversion of the sensor analog output

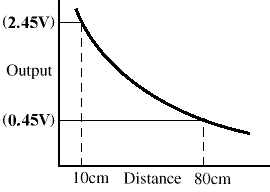
  When powered with a 5V power source, the Sharp sensor has a maximum output
  voltage of about 2.45V, for close distances. The highest useable distance
  gives approximately 0.45V (see Fig. 2). It is therefore wise to use an AD
  converter with two external adjustable voltage references: Vref and COM
  (the one I employed is the MAX148BCAP). In order to obtain the best precision,
  the highest limit of the converter (255 on 8 bits) should more or less correspond
  to the highest output voltage of the sensor, which is the lowest measurable
  distance, and vice versa for the highest reading. In doing so, the full scale of the converter is
  used. Fig. 3 shows the measured result.

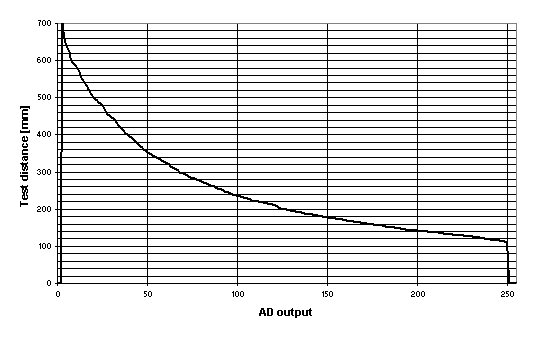
Fig. 3 - GP2D12 output pattern after AD conversion ( 0 ->
~0.45V & 250 -> ~2.45V )

Based on these measurements, a lookup table can be implemented in a microcontroller.
For my own application, I used
a Ubicom SX52 microcontroller
with a 256 entries lookup table.

• Statistical analysis of the sensor output

  In order to measure the noise present on the sensor output, I made some
  tests and statistics with a GP2D12 sensor placed at about 25cm in front
  of a flat white wall. The distribution of 10,000 successive values acquired
  by the microcontroller (at 1kHz) is shown on Fig. 4.

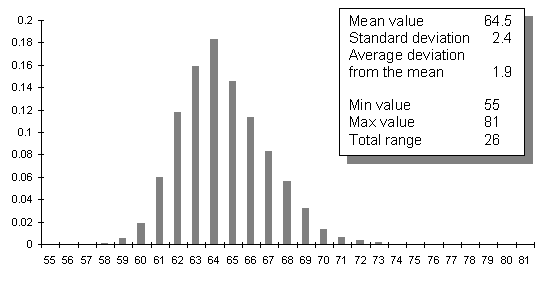
Fig. 4 - Statistical analysis of the Sharp GP2D12 output

The values presented here are characteristic of the GP2D12 output. In particular,
the standard deviation does not depend on the measured distance. However,
the precision of the distance cannot be directly deduced because the output
is non linear. A constant standard deviation over the full range of the sensor
output does not lead to a constant precision of the computed distance.

This graph (Fig. 4) shows that the noise of the Sharp sensor output follows
a normal-like distribution law. Therefore, it would be wise to average several
successive output values to improve the precision.

Note that this quite important noise is essentially due to the sensor itself
(electronic noise). The noise introduced by the converter is marginal. See
Fig. 8 bellow to convince yourself.

• Lookup table for linearization & Precision evaluation

  As the employed 8-bit micro controller is not able to efficiently handle
  multiplications and divisions, a lookup table preferable to convert the
  output values of the sensors into distances (another approach, using a power
  regression, is explained here).
  As the converted values from the AD converter are 8-bit coded, the best
  we can do is to use a lookup table with 256 entries. The microcontroller
  offers the possibility to store 12-bit data in the program memory. It is
  therefore easy to store the distances in millimeters (from 100 to 800), which
  would require 10 bits.

  As the microcontroller doesn't have a lot of program memory, in
  the case of the use of several GP2D12, it seems wise to have a single table
  for all the sensors. The following graph (Fig. 5) shows the measured output
  patterns of 4 different sensors red simultaneously and several times at
  the same distance (only the average for each distances and each sensors
  are shown).

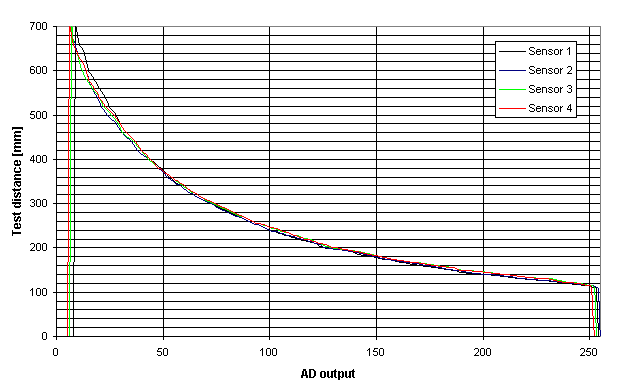
Fig. 5 - Characteristics of four different
Sharp GP2D12 sensors

40 reference distances for each sensor have been defined in order to plot
these graphs. A linear approximation between each pair of successive points
is made. On the following graph (Fig. 6), only the actually measured points
(for one of the four sensors) and their corresponding standard deviation are
shown.

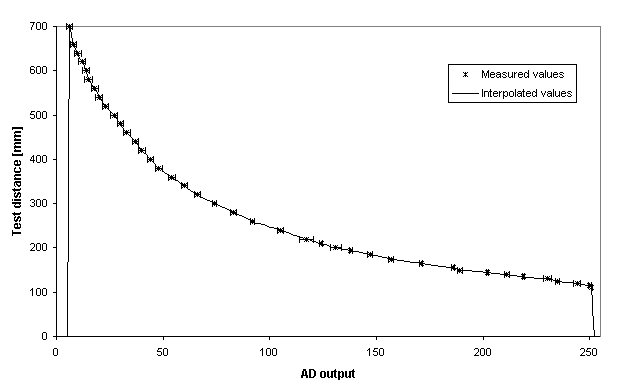
Fig. 6 - Set of 40 measured values and their
corresponding standard deviation

Based on this graph, a rapid evaluation of the precision can
be done. It is easy to understand that the values above 700mm are almost unusable.
At 600mm, the precision is only 20mm and becomes better with closer distance
(about 2mm at 200mm). Of course, using a unique lookup table for several
sensors slightly decreases the precision, but however must represent a good
compromise in certain cases.

• Dynamic distance measurement

  The analog output of the Sharp GP2D12 sensors moves in voltage steps when
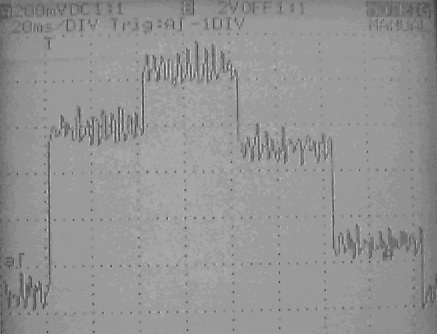
  the measured distance changes. These steps last about 40ms (see Fig. 7).

Fig. 7 - Sharp GP2D12 operation over time

This behavior is certainly due to the fact that it processes an output signal
by internally averaging successive values. Let's assume that the best way
to interpret this signal is to take the step level as the value measured at
its middle. Because there is some noise on the sensor output, we can get an
improved value of the distance by averaging the output along the step.

Fig. 8 shows the typical sensor output during a fast movement of the target
object. As you can see, the noise on the steps can reach about ±100
mV.

Fig. 8 - Sharp sensor output during dynamic
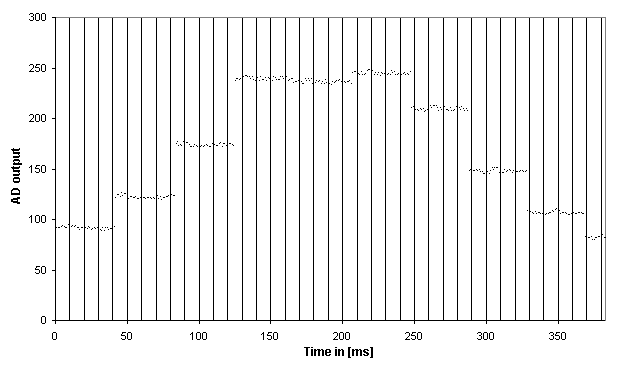
measurement (200mV and 20ms per division)

What is more interesting for us is the same signal seen by the microcontroller
(Fig. 9).

Fig. 9 - Sharp sensor output seen by the
microcontroller during dynamic measurement

The reading frequency of the converter is 1kHz. Therefore the processor can
have an updated value every 1ms and thus about 40 values per step. These 40
values will be averaged over time in order to obtain a good approximation
of the step level without noise (this procedure acts like a digital low-pass
filter). To achieve this, the points belonging to the same steps must be recognized
and clustered.

There are essentially two criteria to achieve this clustering. The first
is certainly the difference between successive data. If the difference is
greater than a specified threshold, the processor can know that it is the
next step. The second one is the maximum time allowable for a step. If two
of them are merged, we can end the set of successive values belonging to the
same step by knowing the maximum length of this set. The maximum number of
conversion during a step is 43. So if there is no significant transition after
43 readings, we can assume that future data are part of the next step. If
some data are not well classified, in this case, this is not so important
because it will not significantly change the mean value of the steps.

If all the steps are at the same height (static case), this clustering process
will lose the synchronization. But, as soon as a transition appears, the algorithm
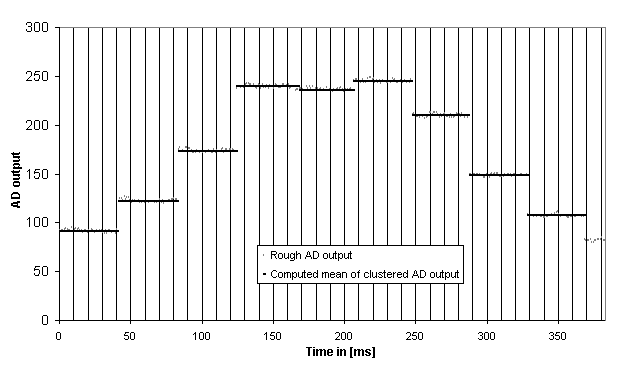
will automatically synchronize again.

This algorithm has been implemented in the microcontroller. The computed
means of the steps are represented in black on Fig. 10. Please note that the
clustering is applied to the rough sensor values and not to the distances
after conversion through the lookup table. This algorithm is intended to filter
the noise of the sensor output, which is constant over the full scale of distances.
If the successive values from the sensor were first converted into distances,
the noise would have not always the same magnitude.

Fig. 10 - Result of the clustering process

The threshold for the difference is set to 15 and the maximum number of points
belonging to the same step was 43.

We can see that there was not enough difference between the fourth and the
fifth steps. Therefore the 43 first points have been allocated to the fourth
step. And the last points (actually 38) before the next recognized transition
are part of the fifth step.

Note that the computation of this average does not require 40 or 43 registers
in memory. A sum variable on 16-bit is updated at each reading of the converter.
When the end of a cluster is detected, the sum is divided by the number of
data in the set. Each computed average will be then transformed into a distance
via the lookup table. This distance is time stamped with the middle of the
previous step.

• Dynamic measurement summary

  To sum up, we have now an algorithm, which is able to process the rough
  sensor data at 1kHz and output an enhanced distance value about each 40ms
  i.e. at a frequency of 25Hz, which is the update rate of the Sharp GP2D12.

  On the following graph (Fig. 11), the whole process is revealed through
  real values coming from the microcontroller in real time.

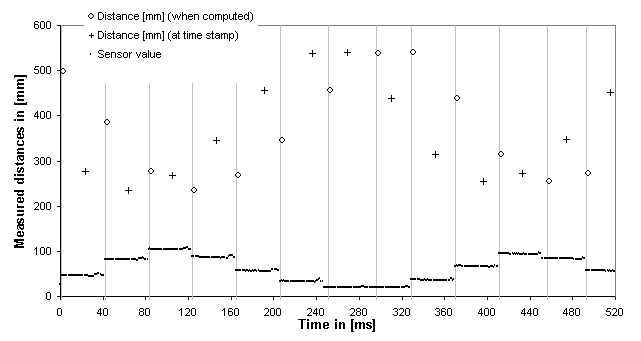
Fig. 11 - Clustering process and resulting
distances

A point represents each acquired sensor value, every millisecond. The vertical
gray lines indicate the moment when the end of a step has been detected: a
jump higher than the specified threshold or the overrun of the maximum successive
values allowable for one step. The little circles symbolize the distances
at the moment they are calculated. The crosses are the same values but plotted
at the position they are time stamped thus 60ms before their calculation.

Now, if several sensors are used, there will be several such processes, asynchronously.
If simultaneous distances must be estimated (that was the case in my project),
it is possible to implement a routine based on the above-described algorithm
(see this document
for further information).

• Related web sites

• GP2D12 data sheet
• The Sharp GP2D02 (digital version) documented by DIDEL:
  www.didel.com/Frames.html?MainFrame=robo/index.html
• Connecting a GP2D12 to an OOPic:
  www.oopic.com/gp2d12.htm
• Contactless Angular Measurement: www.robotprojects.com/ir/angle.htm
• Technical and Calibration Details: www.cs.cmu.edu/~reshko/PILOT/tech_info.html

Your comments
or suggestions are very welcome!