NumPy and ScipPy are very
NumPy and ScipPy are very popular in any scientific use of Python, and rightly so. Practically all scientific libraries, from bioninformatics and biochemistry to physics and astronomy use them. There is even a separate conference for their users!
Yes it seems pretty cool.I
Yes it seems pretty cool.
I started plaing around with VPython and I decided to use that due to it’s simplicity. And it turns out that NumPy is actually an integrated part of VPython.
This paper is really great!
This paper is really great! Not so much because of what they discovered (I didn’t even get there yet), but because it has a very nice summary of what is known so far about quadruped static gaits. I’m in the second chapter and I’ve already found a lot of stuff that I had to learn the hard way myself, plus a lot of stuff that I didn’t know and that I will have to try with my robots. Also a lot of ideas for what can be improved. Thank you.
Yeah it’s awesome.I think
Yeah it’s awesome.
I think these subjects have a very steep learning curve because when you google it a lot of the entries are written by amateurs who may know stuff, but lack the methods of describing it systematically. Other entries on the other hand are written by people who do, but they are experts writing for other experts, and therefore very hard to understand.
What I like about this paper is how thorough it is and at the same time extremely well written and (for the most part) easy to understand, because it explains everything step by step very systematically, and without presuming too much about the reader.
As I mentioned I want to
As I mentioned I want to create a 3D model of my robot to help me understand and visualize the math better. The idea is to end up with an application that besides being the brains of the robot, also visualizes the robot itself, as well as the sensor data.
Last night I was playing around with Visual Python and made this:
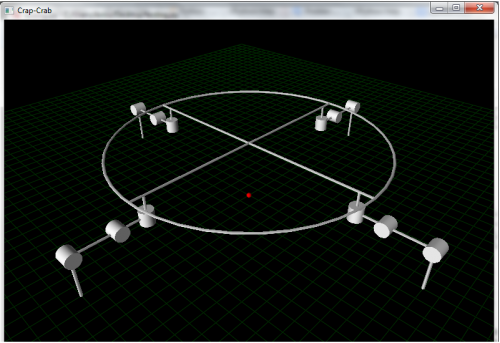
It ain't pretty :) But it isn't supposed to be. I wanted it to be as simple as possible. I didn't use modeling software, I simply draw 3D primitives (lines, cylinders, ring) onto the screen using code.
The idea is to use vectors to represent ..well.. everything. E.g. each leg segment is represented by a vector, and the leg is then drawn onto the screen based on this vector. There will also be a vector representing the axis of each servo (the cylinders). This way when I wan't to move a servo I simply use the function rotate() provided by VPython. E.g. if A is the leg segment vector, B is the servo axis vector and I want to rotate theta degrees, I'll simply write: A.rotate(theta,B). And that's it.
Also if I want to know the position of the end point (or any other point) of a leg given the servo positions (aka Forward Kinematics), it's simply a matter of adding the leg segment vectors up to that point. E.g. if A is the coxa, B the femur and C the tibia, then the simple vector sum A+B+C would give me the end point position.
As mentioned before I'll be using different frames. One for each leg, one for the robot itself and the "world" frame. As it turns out translating between these frames is actually pretty simple (if I understand it correctly), using a translation matrix:
For instance the leg segment and servo positions are given relative to the leg frame, and the leg position relative to the robot frame. If I want to know the leg segment and servo positions relative to the robot frame, I simply solve this matrix with (x,y,z) being the respective positions of leg segments and servos relative to the leg frame, and (dx,dy,dz) being the position of the leg relative to the robot frame. And that should be it.
There are still several things I'm having trouble wrapping my head around though. For instance... in Forward Kinematics you always have exactly one solution. But in Inverse Kinematics you may have no solution or many/infinite solutions. Not sure how to manage this yet?!
Anyway that will be it... for now :P
To Deshipu:It would seem our
To Deshipu:
It would seem our projects are somewhat similar. We`re both making a quadruped of similar configurations. We both wanna use a Python application as the brains of the robot, sending instructions and receiving sensor data to/from the Arduino. And we both want this application to visualize different sensor data.
Anyway we could, as far as the Python application goes, make this a joint venture. This off course would require a certain amount of communication/coordination, so I’m not sure to which degree we should develop together or simply share code/ideas. Either way I’ll create a blog for this project and will be uploading my code there regularly.
Collaboration
It’s complicated 
On one hand, I do want to make a general-purpose python library with different gaits that you could use to control your robot. I even started on it already, it’s called pyambulate and so far only has the basic creep. I hope to get it to a state in which it is stable enough for collaboration, but I’m afraid that the paper you linked will make me change a lot now to make it more general. In any case, this is a good project to collaborate on, I think, once I make a release.
I would also be happy to use the visualisation software that you are developing, and I’m sure I would contribute to it wherever I see the opportunity – just put it on github or bitbucket, and then you can accept or reject patches.
On the other hand, I don’t know where I want to go with my robots and what I want to do with them exactly. I’m just having fun playing with them, and implementing random ideas. I don’t want a more rigid approach, because I’m afraid that it would bore me and make me do something else. I do have ideas for trying different robot configuration, in particular a crab with 2DOF legs that would still use inverse kinematics, and a 2DOF quadruped in the mammalian configuration. But I digress. I don’t want to collaborate on that. I also don’t want to make any promises, or take any responsibility. This is my hobby project and I don’t want it to become a burden.
I hope you don’t mind me being honest about it.
1st off… Honesty rules, so
1st off… Honesty rules, so off course I don’t mind 
2nd… It was never my intention to intertwine our respective robotics activities completely. For me this is also just fun, and I wouldn’t wanna make too many promises or adapt a more rigid approach. God forbid 
However it could perhaps be beneficial to us both to find some level of short term coorporation regarding the BASICS of the Python control application. This application we could then take separate places, yet still share code easily (no strings attached) given the common starting point.
The 1st thing would be identifying what “the basics” mean. It could be simply agreeing on a common approch, such as described below with a separate frame for each leg, the robot and the world. And agreeing on where the origin of the respective frames would be. It could also be finding a general (easily configurable) format for the serial communication. Or agreeing on certain configuration constants in general (e.g. I allready made the length of the respective leg segments configurable).
I actually don’t know right now, but small things like this would allready facilitate sharing code (e.g. a gait), without actually coorporating, in the future.
Anyway we’ll see how things work out
As mentioned I wanna create
As mentioned I wanna create a Python application that visualizes the robots movements. I started by creating one for the kinematics (forward + inverse) of a leg.
The idea is that the user can enter an angle for each servo, and the program calculates and shows the corresponding leg movements (aka forward kinematics). Or the user can enter the coordinates of the foot and the angles will be calculated based on that (aka inverse kinematics).
So far the forward kinematics work pretty well, but I'm having problems implementing the inverse kinematics using the formulas above in the topic description. Calculating gamma works fine (with a little twist), but alpha0, alpha1 and beta return some strange values that I can't make sense of.
I know it's a long shot since running the program requieres VPython (which probably very few here have), but if someone can see what I'm doing wrong it would be awesome, so I uploaded the code to here. Most of the code is irrelevant though (creating user interface and drawing, etc.). The function in question is called calc_inv(). Here is the part that implements the formulas:
# Calculate c (gamma)
c = 90
if z > 0: c = degrees(arctan(x/z))
elif z < 0: c = 180+degrees(arctan(x/z))
# Auxiliary calculations
h = abs(y)
h2 = h*h
l = sqrt(x*x+z*z)
k = (l-COXA)*(l-COXA)
fem2 = FEMUR*FEMUR
tib2 = TIBIA*TIBIA
# Calculate a0 and a1 (alpha)
a0 = arctan((l-COXA)/h)
a1 = arccos( (fem2+k+h2-tib2)/(2*FEMUR*sqrt(k+h2)) )
# Calculate b (beta)
b = arccos( (tib2+fem2-h2-k)/(2*FEMUR*TIBIA) )
I should perhaps mention that I'm working with a different coordinate system than that above, meaning that for me the x-axis is horizontal, the y-axis is vertical and the z-axis is the depth. That is why y and z are interchanged in my code.
Use a repository
I really recommend to use a code repository right from the beginning. You can put it on bitbucket or github and not only easily link to your code and to its individual lines, but also receive pull requests with proposed changes, and discuss individual lines of code in those. You will also have a full history of your code’s development, and you will be able to always get back to a working version. Not to mention a backup, in case something happens to your computer. It seems complicated, but to start you only really need to know three commands: init, commit and push.
As for your formulas, the way they are rolled all rogether into a single formula makes them rather hard to understand and analyze. Have you tried my code? You are free to use it.
I tried analyzing the
I tried analyzing the formulas and came up with something like this:
import mathdef _solve_triangle(a, b, c):
a, b, c = abs(a), abs(b), abs©
if a + b < c or a + c < b or b + c < a:
raise ValueError(“Impossible triangle: %r, %r, %r” % (a, b, c))
cos = float(a ** 2 + b ** 2 - c ** 2) / (2 * a * b)
return math.acos(cos)def _norm(a, b):
return math.sqrt(a ** 2 + b ** 2)j = _norm(x, y)
k = j - coxa
d = _norm(z, k)
sigma = math.atan2(x, y)
alpha0 = math.atan2(k, z)
alpha1 = _solve_triangle(d, femur, tibia)
beta = _solve_triangle(tibia, femur, d)
Please note, that it doesn’t correspond to those formulas exactly – I think he made a mistake assuminig that (a + b)² == (a² + b²), but I’m not sure.
Hey thanks for the reply…I
Hey thanks for the reply…
I tried using the code you posted above (not sure whether you refferred to that when you wrote “Have you tried my code?”). It doesn’t work either.
The thing is… Beta (the ankle angle) is calculated correctly ONLY when the knee angle is at 90. In other words the ankle angle changes when the knee angle changes, which it shouldn’t. BTW the Betas calculated by my original code and your code are the same.
The Alpha angles returned are diiferent though, but in either case I can’t make much sence of the values.
"As for your formulas, the way they are rolled all rogether into a single formula makes them rather hard to understand and analyze."
I thought the same thing, which is why I started from scratch trying to piece it together bit by bit, which isn’t so easy though because every explanation I read is very different in their approach.
Ah I also tried implementing this version but it didn’t work either 
About the repository… Yeah well I’ll get around to that. Not sure how beneficial it would be at this stage though. Just playing around with some code and some math. Still not actually developing anything. But later…
Good and bad news
The good:
There is nothing wrong with the formulas it would seem. I now tried many different approaches (including making my own from scratch) and they generally return the same values. So my conclusion is that the formulas are ok.
The bad:
That off course means I wasted a couple of hours looking the wrong places for answers. Obviously something is wrong with my code , but since it isn’t the IK math it must be elsewhere, which at this point I haven’t got a clue where is.
Important question:
We do agree that the angle of the knee (green servo / alpha) does NOT affect the angle of the ankle (blue servo / beta)? Don’t we?
Well cause that’s one of the things that I thought was wrong with the formulas. Beta is only calculated correctly when alpha is at 90 degrees 
Damn! Now that I think I
Damn! Now that I think I finally understand the theory of this, I just can’t make the numbers behave
In reality the angle of the hip servo does not affect the rest of the IK calculations. So we have the following (side view):
This we can regard as a simple triangle like this:
The following we know: a = Tibia and b = Femur.
Furthermore c is the distance between the knee servo and the foot (P), thus it can be calculated easily. One way is the following:
c = sqrt( x² + z² ) - Coxa
c = sqrt( y² + c² )
Then the law of cosines tells us that:
C = acos( (a² + b² - c²) / (2*a*b) )
So now we have calculated Beta. BUT this is where it all goes wrong for me. Beta changes depending on the angle of the knee. This cannot be right because by altering the knee angle we're simply rotating the entire triangle, and NOT changing it's dimensions. I've been trying different ways of doing the math, but to no avail, still the same.
Does anyone have a clue why this is happening?
Hehe… Never mind… I
Hehe… Never mind… I found a very subtle but very nasty little hidden bug in the FORWARD kinematics code, which I had earlier suspected was there but just couldn’t see. So the error after all was NOT in the inverse kinematics calculations. It was all because I used flawed code to test well functioning code. Please slap me
Anyway all is well Sorry about my rambling…
It’s not all for nothing,
It’s not all for nothing, because you have learned a lot in the process! I bet now you can write IK code from scratch with your eyes closed for any leg confuguration. As for the bug always being where you are not looking – that’s basically what programming is. It happens all the time, so don’t worry about it.
Translation
Ah I forgot to mention that I made a function based on the translation matrix I mentioned earlier. I’ve used it quite a bit and It works well.
# Translate vector according to displacement vector
def translate(v, dv):
m = matrix([[1,0,0,dv.x],[0,1,0,dv.y],[0,0,1,dv.z],[0,0,0,1]])
x = matrix([[v.x],[v.y],[v.z],[1]])
b = m*x
return vector(b.item(0), b.item(1), b.item(2))
Now off course I’m using NumPy which allows me to do matrix multiplication simply with the *-operator, but even if you’re not it’s pretty easy to do “manually”. There is no trig math. Just + and *. From what I’ve read this way of translating is indeed more precise than using spherical coordinates as Deshipu mentioned earlier
Hehe… This is really hard
Hehe… This is really hard to get working… BUT I think I finally know why… When x is NEGATIVE everything gets messed up. This is perhaps because of the way I set up the angles to begin with. Anyway when x is positive everything is calculated perfectly now (I think). And now I know what the problem is I can calculate the final angles differently when x is negative.
This is the code I’m using currently:
# Calculate hip angle (gamma)
c = atan2(abs(x),z)
# Calculate distance from knee to foot
d = sqrt(x2+z2)-COXA
d = sqrt(y2+d2)
# Calculate ankle angle (beta)
b = acos( (TIBIA2+FEMUR2-d2) / (2TIBIAFEMUR) )
# Calculate knee angle (alpha)
a0 = atan2( (sqrt(xx+zz)-COXA), abs(y) )
a1 = acos( (FEMUR2+d2-TIBIA2) / (2FEMURd) )
# Set angles
_hip = degrees©
_knee = 180-degrees(a0)-degrees(a1)
_ankle = 180-degrees(b)
PS: Yes I will simplify the code later using functions and auxiliary calculations, but for now I prefer it like this
Ok now that I got the leg
Ok now that I got the leg part going I started making the app for the entire robot. The first thing I wanna do is to write code for the following movements: Tilt, sway, twist and hover (lifting the body up and down). All these movements should be done with the feet staying put in one place on the ground.
Here is how I see it: The funny thing is that from the leg’s point of view it is moving the foot allthough it’s staying put, since in general the legs don’t know where the ground is or anything else pertinent to the robot/world frame. They simply receive a foot postion, move there (using IK), and that’s it.
The robot simply decides where it’s body should be positioned, and since it knows where the legs are connected, as well as the current foot positions, it can then calculate the new foot positions (using a translation matrix, etc.) and pass them on to the legs.
Is that pretty much how you guys see it too?
PS: A couple of unrelated questions for Deshipu: I’m using Python 64 bit and I need some libs for (1) joystick handling and (2) serial communication. After some googling it turns out that the obvious choice would be the libs PySerial and PyGame (for joystick). BUT apparently these libs do not have release versions for 64 bit. So I got the options of (1) using pre-release versions or (2) start using a 32 bit version of Python. Did you have the same considerations? If so then what did you do?
PPS: This thread is turning rather epic allthough there are only the 3 of us commenting. I that why it’s no longer visible on the “recent posts” page?
Hmmm… I’m trying to put
Hmmm… I’m trying to put this all together, but I still can’t figure out whether it’s beneficial to operate with a frame for the robot or whether it’s easier just to operate with the 4 leg frames and a world frame. In the end what did you guys end up doing?
